そこで、今回は、比例代表の制度を少しだけくわしめに解説します。なぜ、今回、中道改革連合の元立憲議員が、比例名簿順位の件で戦々恐々としているのか、その理由もわかりますよ。
1,小選挙区と比例代表の並立
◇小選挙区と比例代表の合計465議席をめぐる戦い
ご存じのとおり、衆議院は「小選挙区」と「比例代表」の並立制を採用しています。2026年現在の衆議院総選挙では、以下の議席数を小選挙区と比例にわかれ、各候補者が争うことになります。
小選挙区:289議席
比例代表:176議席
→ 合計 465議席
つまり、過半数は233議席です。
◇小選挙区制度のルール
小選挙区制の仕組みについては簡単で、1つの選挙区から1人しか当選できないというルールです。各選挙区からは1人しか当選できませんので、投票行動や政党の動向が自然と有力2党に集約されていきます。この「小選挙区制(相対多数投票制)は二大政党制をもたらす」という法則を政治学の世界では、デュヴェルジェの法則といいます。ですが、もちろん、高校入試には出題されません(では、なぜ現在の日本の政治状況が2大政党制に向かっていないのかという問題については別の機会に)。
2,比例代表の選挙区(ブロック)
衆議院総選挙では、全国を11の比例ブロックに分けて実施します。
各ブロックの定数(議席数)は人口に応じて決まっており、ブロック別の定数は、北海道8、東北12、北関東19、南関東23、東京19、北陸信越10、東海21、近畿28、中国10、四国6、九州20となっています。そうです、実は、近畿ブロックが全国で最大人数なのです。わたしたち兵庫県民の比例票は、この近畿ブロックに反映されます。
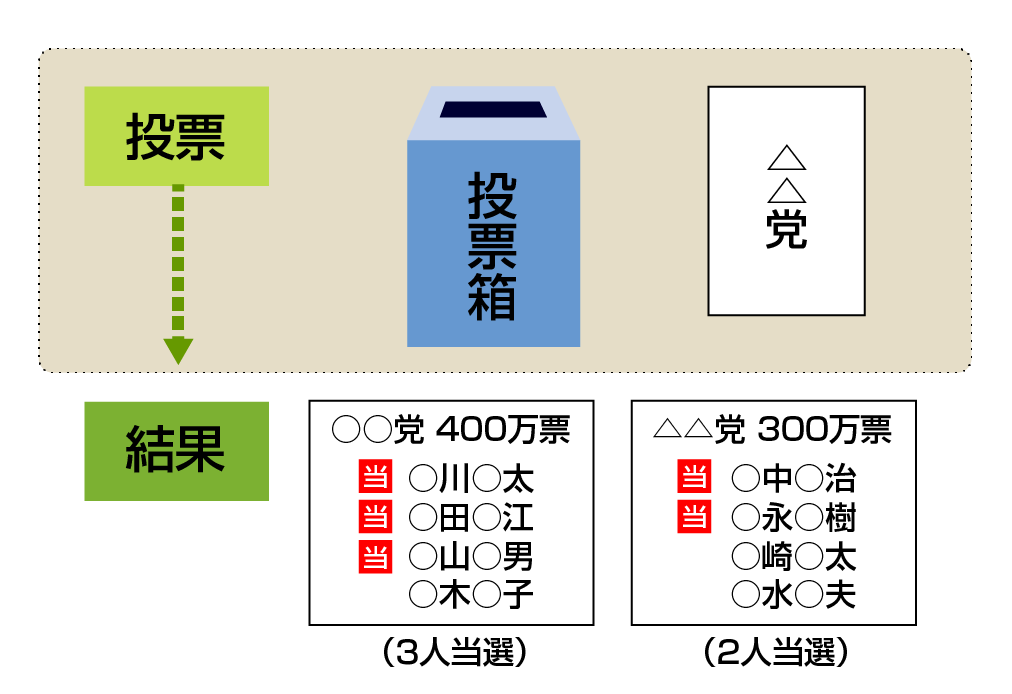
3,ドント方式で配分
次に、各党が獲得した票を「ドント方式」と呼ばれる手法で議席数に換算します。それぞれの党の得票数を1で割り、2で割り……と1から順に整数で割っていき、全党の計算結果(商)を大きい順に並べるという方法で、高校入試でもお馴染みですね。上位から定数の枠内に入っている商の個数が、その党に割り振られる議席数となります。
4,獲得議席数と比例名簿順位
さて、重要なのはここからです。政治山さんの素晴らしくわかりやすいサイトを引用させていただきながら、解説していきます。(https://seijiyama.jp/article/news/nws20141212-012.html)。
衆議院議員選挙では、小選挙区と比例代表の両方に立候補(重複立候補といいます)できるため、各党が作成する比例名簿には、比例代表のみの候補者と重複立候補者が共存する場合があります。今回の選挙でいえば、旧公明党の議員は比例代表のみの候補者ですね。比例代表のみの候補者は名簿順位が決まっていますが、重複立候補者の場合は、名簿順位を政党が決めるケースと小選挙区の戦績によって決まるケースに分かれます。
◇名簿順位が上位だと圧倒的優位に立つ
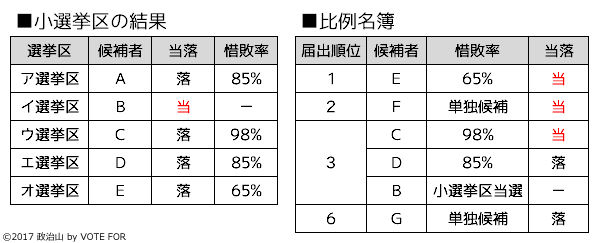
ここで重要なのは、比例の名簿順位を同一にできるという点です。以下の図を見てください。同一3位にB、C、Dをおいています。このとき、B、C、Dの誰に議席を配分するかという指標には「惜敗率」を用います。惜敗率とは、小選挙区で落選した候補者の得票数を、同一選挙区での当選者の得票数で割って算出する計算方法です。つまり、惜敗率が高ければ、議席獲得の可能性が上がるわけです。同一順位のなかの争いだけをみれば、民意を反映したフェアな方法といえます。
問題は、ここからです。〇〇党が比例で3議席を獲得し、以下の図の結果となった場合、重複立候補の当選者は次のように決まります。
(1)小選挙区の結果
・小選挙区で当選したB候補の当選が確定
・小選挙区のみに立候補して落選したA候補の落選が確定
(2)比例代表の結果
・小選挙区と比例代表に重複立候補している候補(B、C、D、E)の惜敗率を計算
・惜敗率を元に比例名簿の順位を決める
(3)名簿順位の上位者から当選を決定
この〇〇党は比例代表で3議席獲得しましたので、名簿順位の上位3人(E、F、C)の当選が決定。
みなさん、恐ろしい制度だと感じませんでしたか?? E候補は惜敗率が低くても名簿順位が1位のため当選し、F候補は比例単独候補で名簿順位も2位のため当選してしまうわけです。ちなみに、G候補は、小選挙区にも出馬せず、比例名簿も最下位なので、はじめから勝ち目はほぼほぼない状況です。
さて、今回の総選挙、中道改革連合の旧公明党議員の皆さんは、小選挙区への出馬を辞退した代わりに比例名簿の1位、2位をほぼ独占しています。比例名簿順位の重要性がおわかりいただけたでしょうか?
学習塾グルントラーゲでは、ときに、入試に出ない内容であっても、生徒にいろいろなことに興味をもってもらうきっかけをつくるため、わかりやすく、面白く教えることを心がけています。一度、体験授業の方、来てみませんか??
兵庫県川西市向陽台2-2-3
学習塾グルントラーゲ